8. ကိုဩဒိနိတ်ရည်ညွှန်းစနစ်များ (Coordinate Reference Systems)

	ရည်ရွယ်ချက်များ	Coordinate Reference System များအကြောင်း နားလည်စေရန်။
	Keyword များ	Coordinate Reference System (CRS) ၊ Map Projection ၊ On the Fly Projection ၊ Latitude ၊ Longitude ၊ Northing ၊ Easting

8.1. အကျဉ်းချုပ် (Overview)

မြေပုံအရိပ်ချစနစ်များ (Map projections) သည် ကမ္ဘာ့မြေမျက်နှာပြင် သို့မဟုတ် ကမ္ဘာကြီး၏ အပိုင်းတစ်ခုကို စာရွက်ပေါ်တွင် သို့မဟုတ် ကွန်ပျူတာမျက်နှာပြင်ပေါ်တွင် ဖော်ပြခြင်းဖြစ်သည်။ Layman ၏အသုံးအနှုန်းအရ မြေပုံအရိပ်ချစနစ်များသည် ကမ္ဘာကြီး၏ စက်လုံးပုံသဏ္ဍာန် (3D) မှ အပြန့် ပုံသဏ္ဍာန် (2D) သို့ပြောင်းလဲခြင်းဖြစ်သည်။

ကိုဩဒိနိတ်ရည်ညွှန်းစနစ် (CRS) တစ်ခုသည် GIS ထဲရှိ 2D မြေပုံနှင့် ကမ္ဘာပေါ်ရှိ လက်တွေ့နေရာများနှင့် ဆက်နွယ်ပုံကို သတ်မှတ်ပေးပါသည်။ မည်သည့် မြေပုံအရိပ်ချစနစ်နှင့် မည်သည့် CRS ကိုအသုံးပြုရမည်မှာ သင်အလုပ်လုပ်လိုသော ဧရိယာ၏နယ်ပယ်အကျယ်အဝန်း၊ လုပ်ဆောင်လိုသော ဆန်းစစ်လေ့လာမှုနှင့် data ရရှိနိုင်မှုများ အပေါ်တွင် မူတည်ပါသည်။

8.2. မြေပုံအရိပ်ချစနစ်အကြောင်း အသေးစိတ် (Map Projection in detail)

ကမ္ဘာကြီး၏ပုံသဏ္ဍာန်ကို ဖော်ပြသည့် သမားရိုးကျနည်းလမ်းတစ်ခုမှာ ကမ္ဘာလုံး (globe) ပုံသဏ္ဍာန်ဖြင့်ဖော်ပြခြင်းဖြစ်သည်။ သို့သော် ထိုနည်းလမ်းနှင့်ပတ်သက်ပြီး ပြဿနာတစ်ခုရှိပါသည်။ ကမ္ဘာလုံးများသည် ကမ္ဘာကြီး၏အဓိကပုံသဏ္ဍာန်အတိုင်း ပြသနိုင်ပြီး ကမ္ဘာ့တိုက်ကြီးများအရွယ်အစားရှိသော feature များကို တည်နေရာအရ ပုံဖော်ပြသနိုင်သော်လည်း အိတ်ထဲသယ်ဆောင်သွားရန် လွန်စွာခက်ခဲပါသည်။ ၎င်းတို့ကို အလွန်သေးငယ်သော စကေးများ (ဥပမာ- 1: 100 million) တွင် အသုံးပြုလျှင်သာ အဆင်ပြေမည်ဖြစ်ပါသည်။

GIS application များတွင် အသုံးများသော thematic (အကြောင်းအရာကိုဖော်ပြသော) မြေပုံ data အများစုသည် စကေးကြီးကြပါသည်။ ပုံမှန် GIS dataset များတွင် အသေးစိတ်မြင်ရမှုအဆင့်ပေါ်မူတည်၍ 1:250 000 သို့မဟုတ် ပိုကြီးသော စကေးများရှိကြပါသည်။ ထိုအရွယ်အစားရှိသော ကမ္ဘာလုံးတစ်ခုကို ထုတ်လုပ်ရာတွင် ခက်ခဲပြီး အကုန်အကျများနိုင်ပါသည်၊ သယ်ယူသွားရန် ပိုလို့ပင် ခက်ခဲပါလိမ့်မည်။ ထို့ကြောင့် မြေပုံရေးဆွဲသူများသည် map projections ဟုခေါ်သော နည်းစနစ်ကို ဖန်တီးပြီး စက်လုံးပုံစံကမ္ဘာကြီးကို သင့်တင့်သောတိကျမှုရှိသည့် နှစ်ဘက်မြင် (2D) အနေဖြင့် ပြသကြပါသည်။

ကမ္ဘာကြီးကို အနီးကပ်ကြည့်ပါက အတော်အသင့်ပြားနေသည့်ပုံစံ ဖြစ်နေပါသည်။ သို့သော် အာကာသမှကြည့်သောအခါ ကမ္ဘာကြီးသည် အတော်အသင့်လုံးဝန်းနေသည်ကို မြင်တွေ့နိုင်ပါသည်။ နောက်လာမည့်ခေါင်းစဉ်ဖြစ်သော မြေပုံထုတ်လုပ်ခြင်းအပိုင်းတွင်တွေ့ရမည့် မြေပုံများသည် လက်ရှိဖြစ်တည်မှုကို ကိုယ်စားပြုဖော်ပြခြင်းများဖြစ်သည်။ Feature များကို ကိုယ်စားပြုဖော်ပြရန်သာမက ၎င်းတို့၏ပုံသဏ္ဍာန်နှင့် တည်နေရာအရစီစဉ်ထားရှိမှု များကိုလည်း ကိုယ်စားပြုဖော်ပြရန် မြေပုံများကို ဒီဇိုင်းရေးဆွဲထားပါသည်။ Map projection တစ်ခုချင်းစီတွင် အားသာချက်များ နှင့် အားနည်းချက်များ ရှိကြပါသည်။ မြေပုံတစ်ခုအတွက် အကောင်းဆုံး projection သည် မြေပုံ၏ စကေး နှင့် မြေပုံကိုအသုံးပြုမည့် ရည်ရွယ်ချက်အပေါ် မူတည်ပါသည်။ ဥပမာ- projection တစ်ခုကို အာဖရိကတိုက်တစ်ခုလုံးကို မြေပုံဆွဲရန် အသုံးပြုသောအခါ လက်မခံနိုင်သော distortion (ပုံသဏ္ဍာန်ပျက်မှု) များရှိနိုင်သော်လည်း သင့်နိုင်ငံအတွက် စကေးအကြီး (အသေးစိတ်) မြေပုံ တစ်ခုရေးဆွဲရန်အတွက် ၎င်းသည် အကောင်းဆုံး projection တစ်ခုဖြစ်နိုင်ပါသည်။ Map projection တစ်ခု၏ဂုဏ်သတ္တိများသည် မြေပုံ၏ ဒီဇိုင်း feature အချို့ကိုလည်း လွှမ်းမိုးမှုရှိနိုင်ပါသည်။ အချို့ projection များသည် ဧရိယာငယ်များအတွက် ကောင်းမွန်ပါသည်၊ အချို့ projection များသည် အရှေ့-အနောက် extent ကြီးမားသော ဧရိယာများကို မြေပုံဆွဲရာတွင် ကောင်းမွန်ပြီး အချို့သည် မြောက်-တောင် extent ကြီးမားသော ဧရိယာများကို မြေပုံဆွဲရာတွင် ပိုကောင်းပါသည်။

8.3. မြေပုံအရိပ်ချစနစ် အုပ်စု ၃ မျိုး (The three families of map projections)

Map projection ဖန်တီးခြင်းလုပ်ငန်းစဉ်ကို အကောင်းဆုံးပုံဖော်ပြသသည့်နည်းလမ်းမှာ ဖောက်ထွင်းမြင်ရသော ကမ္ဘာလုံးတစ်ခု၏ အထဲတွင် မီးအလင်းတစ်ခုဖြင့် ထိုးထားပြီး ကမ္ဘာပေါ်ရှိ feature outline များကို စာရွက်အပြန့်ပေါ်တွင် ပုံရိပ်ချခြင်းဖြစ်သည်။ ကမ္ဘာလုံး၏ပတ်လည်တွင် cylindrical (ထုလုံးရှည်) ပုံစံအနေဖြင့်၊ cone (ကတော့ချွန်) ပုံစံဖြင့် သို့မဟုတ် flat surface (မျက်နှာပြင်အပြား) ဖြင့် ဝိုင်းရံပြီး မတူညီသောနည်းလမ်းများဖြင့် အရိပ်ချခြင်းလုပ်ဆောင်ကြပါသည်။ အဆိုပါ နည်းလမ်းများထဲမှ တစ်ခုချင်းစီသည် map projection family (မြေပုံအရိပ်ချစနစ်အုပ်စု) တစ်ခုကို ထုတ်ပေးပါသည်။ ထို့ကြောင့် planar projections အုပ်စု၊ cylindrical projections အုပ်စုနှင့် conical projections အုပ်စုဟူ၍ ရှိပါသည် (Fig. 8.16 တွင်ကြည့်ပါ)။

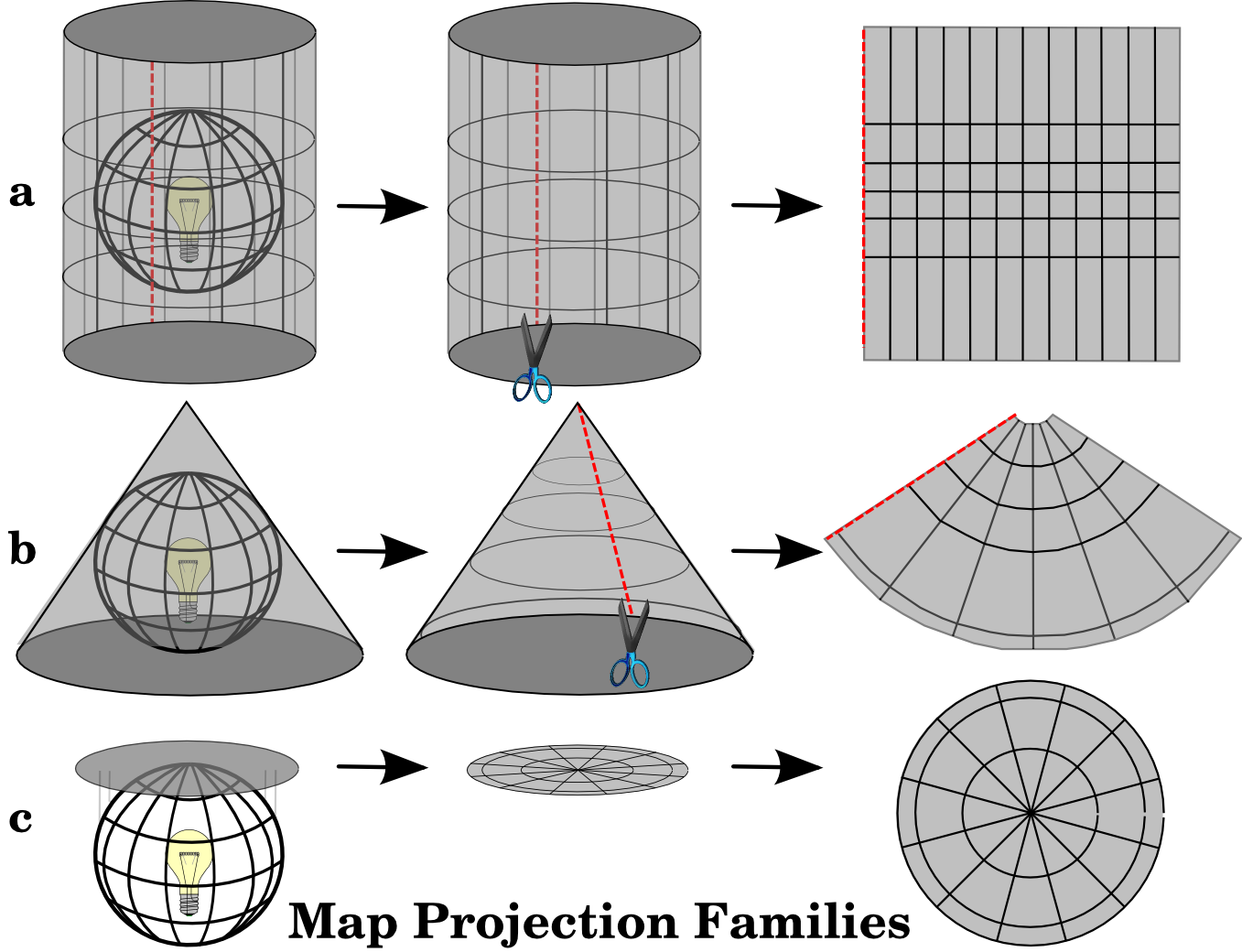
../../_images/projection_families.png — Fig. 8.16 မြေပုံအရိပ်ချစနစ်အုပ်စု ၃ မျိုး။ a) cylindrical projections ၊ b) conical projections သို့မဟုတ် c) planar projections

ယနေ့ခေတ်တွင် လုံးဝန်းသောကမ္ဘာကြီးကို စာရွက်အပြန့်ပေါ်သို့ အရိပ်ချခြင်း လုပ်ငန်းစဉ်ကို ဂျီဩမေတြီနှင့် တြီဂိုနိုမေထြီ သင်္ချာနိယာမများအသုံးပြုပြီး လုပ်ဆောင်ကြပါသည်။ ၎င်းသည် ကမ္ဘာလုံးကိုဖြတ်သော အလင်း၏ အရိပ်ချခြင်းကို ပြန်လည်ဖန်တီးပေးပါသည်။

8.4. မြေပုံအရိပ်ချစနစ်များ၏ တိကျမှု (Accuracy of map projections)

Map projection များသည် လုံးဝန်းသော ကမ္ဘာကြီးကို လုံးဝအတိအကျ ကိုယ်စားပြုဖော်ပြနိုင်မည်မဟုတ်ပါ။ Map projection လုပ်ငန်းစဉ်တစ်ခု၏ရလာဒ်အနေဖြင့် မြေပုံတိုင်းသည် ထောင့်မှန်ကန်မှု၊ အကွာအဝေး နှင့် ဧရိယာတို့၏ distortion များကိုပြသပေးပါသည်။ Map projection တစ်ခုသည် အဆိုပါ ဝိသေသလက္ခဏာများစွာကို ပေါင်းစပ်ထားသည်လည်းဖြစ်နိုင်သလို ဧရိယာ၊ အကွာအဝေးနှင့် ထောင့်မှန်ကန်မှု distortion များကို လက်ခံနိုင်သည့်အကန့်အသတ်အချို့အတွင်း ညှိထားသော (compromise) projection တစ်ခုလည်းဖြစ်နိုင်ပါသည်။ ထိုသို့ ညှိထားသော projection ဥပမာများမှာ Winkel Tripel projection နှင့် Robinson projection တို့ဖြစ်ပြီး ၎င်းတို့ကို ကမ္ဘာမြေပုံများရေးဆွဲခြင်းနှင့် ပုံဖော်ပြသခြင်းတွင် အသုံးပြုလေ့ရှိပါသည်။

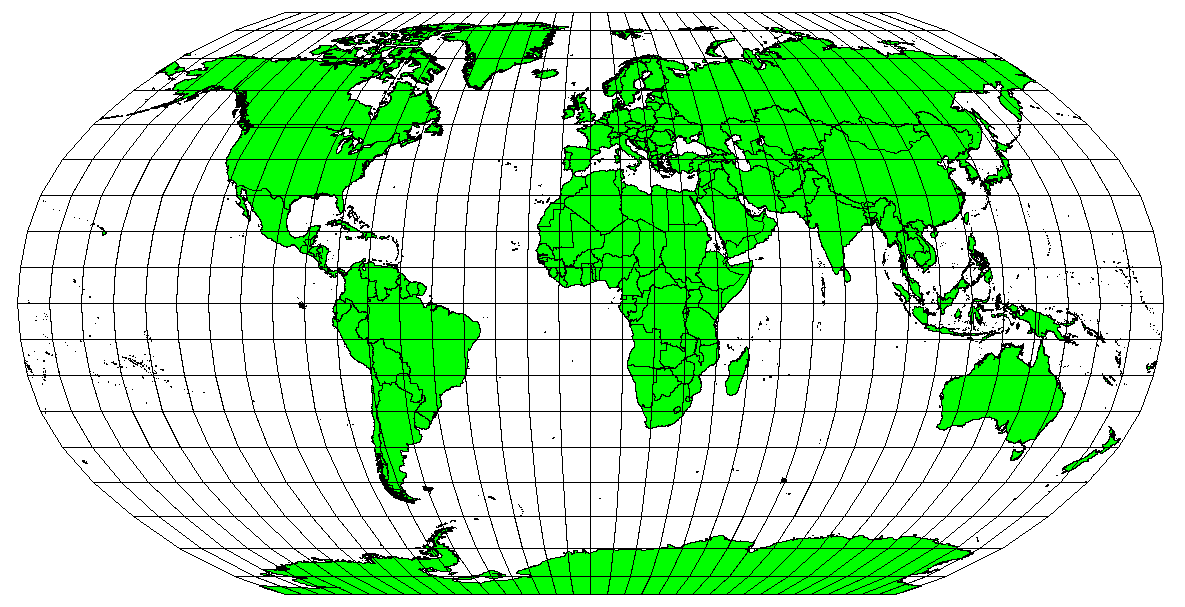
../../_images/robinson_projection.png — Fig. 8.17 Robinson projection သည် ဧရိယာ၊ ထောင့်မှန်ကန်မှုနှင့် အကွာအဝေး distortion များကို လက်ခံနိုင်သော compromise projection တစ်ခုဖြစ်ပါသည်။

Map projection တစ်ခုထဲတွင် ဝိသေသလက္ခဏာအားလုံးကို မှန်ကန်အောင် အချိန်တည်း ထိန်းထားရန်မဖြစ်နိုင်ပါ။ ဆိုလိုသည်မှာ သင်သည် တိကျသောဆန်းစစ်လေ့မှုတစ်ခုလုပ်ဆောင်လိုပါက သင့်ဆန်းစစ်လေ့လာမှုအတွက် အကောင်းဆုံးဖြစ်သော ဝိသေသလက္ခဏာရှိသည့် map projection တစ်ခုကိုအသုံးပြုသင့်ပါသည်။ ဥပမာ- မြေပုံပေါ်တွင် အကွာအဝေးများကို တိုင်းတာလိုပါက အကွာအဝေးအတွက်တိကျမှုကောင်းမွန်သော map projection ကိုအသုံးပြုသင့်ပါသည်။

8.4.1. ထောင့်တန်ဖိုးများမှန်ကန်သော မြေပုံအရိပ်ချစနစ်များ (Map projections with angular conformity)

ကမ္ဘာလုံးတစ်ခုတွင် သံလိုက်အိမ်မြှောင်၏ အဓိကလားရာများသည် (မြောက်၊ အရှေ့၊ တောင် နှင့် အနောက်) တစ်ခုနှင့်တစ်ခု ၉၀ ဒီဂရီတွင် အမြဲတမ်းဖြစ်ပေါ်ပါလိမ့်မည်။ တစ်နည်းအားဖြင့် အရှေ့ဘက်သည် မြောက်ဘက်၏ ၉၀ ဒီဂရီထောင့်တွင် အမြဲဖြစ်ပေါ်ပါလိမ့်မည်။ Map projection တစ်ခုတွင်လည်း ထောင့်ဆိုင်ရာ ဂုဏ်သတ္တိများ မှန်ကန်စေရန် ထိန်းသိမ်းပေးထားနိုင်ပါသည်။ ထိုသို့သော ထောင့်တန်ဖိုးများမှန်ကန်သော map projection ကို conformal သို့မဟုတ် orthomorphic projection ဟုခေါ်ပါသည်။

ထောင့်ဆက်နွယ်မှုများ အရေးကြီးသည့်ကိစ္စမျိုးတွင် အဆိုပါ projection များကို အသုံးပြုကြပါသည်။ ၎င်းတို့ကို လမ်းညွှန်ပြသခြင်း သို့မဟုတ် မိုးလေဝသ လုပ်ငန်းများအတွက် အသုံးများကြပါသည်။ မြေပုံတစ်ခုပေါ်တွင် ထောင့်အမှန်များ ဖြစ်သောထိန်းထားခြင်းသည် ကြီးမားသောဧရိယာများအတွက် ခက်ခဲပါသည်၊ ထို့ကြောင့် ကမ္ဘာကြီး၏ သေးငယ်သောအပိုင်းများအတွက်သာ လုပ်ဆောင်သင့်ပါသည်။ Conformal projection အမျိုးအစားသည် ဧရိယာများအတွက် distortion ဖြစ်စေပါသည်။ ဆိုလိုသည်မှာ မြေပုံပေါ်တွင် ဧရိယာတိုင်းတာမှုများလုပ်ဆောင်ပါက မှန်ကန်မည်မဟုတ်ပါ။ ဥပမာအားဖြင့် Mercator projection (Fig. 8.18 တွင်ပြထားသည့်အတိုင်း) နှင့် Lambert Conformal Conic projection တို့ဖြစ်ကြပါသည်။ U.S. Geological Survey သည် မြေမျက်နှာသွင်ပြင်ပြမြေပုံများစွာအတွက် conformal projection ကိုအသုံးပြုကြပါသည်။

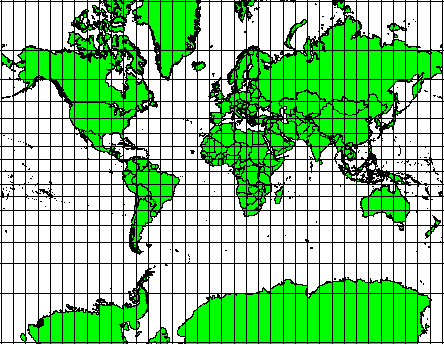
../../_images/mercator_projection.png — Fig. 8.18 ထောင့်ဆက်နွယ်မှုများ အရေးကြီးသည့်ကိစ္စမျိုးတွင် Mercator projection ကိုအသုံးပြုထားပါသည်၊ သို့သော် ဧရိယာဆက်နွယ်မှုများ မှန်ကန်မည်မဟုတ်ပါ။

8.4.2. အကွာအဝေးညီ မြေပုံအရိပ်ချစနစ်များ (Map projections with equal distance)

မြေပုံပေါ်တွင် အကွာအဝေးများကို တိကျစွာ တိုင်းတာလိုပါက အကွာအဝေးဆိုင်ရာများကို ကောင်းမွန်စွာ ထိန်းသိမ်းထားပေးသော projection တစ်ခုကို အသုံးပြုသင့်ပါသည်။ အဆိုပါ projection မျိုးကို equidistant projections ဟုခေါ်ဆိုပြီး မြေပုံ၏ စကေး ကို တည်မြဲအောင် ထိန်းထားပေးရန် လိုအပ်ပါသည်။ Projection ၏အလယ်ဗဟိုမှ မြေပုံပေါ်ရှိ အခြားမည်သည့်နေရာကိုမဆို အကွာအဝေးမှန်ကန်စွာ ပြသနိုင်ပါက မြေပုံသည် equidistant ဖြစ်ပါသည်။ Equidistant projections သည် projection ၏အလယ်ဗဟိုမှ သို့မဟုတ် ပေးထားသောလိုင်းများတစ်လျှောက်မှ တိကျသော အကွာအဝေးများကို ထိန်းထားပေးပါသည်။ ထိုသို့သော projection များကို ရေဒီယိုနှင့် မြေငလျင် ဆိုင်ရာမြေပုံများအတွက်နှင့် လမ်းညွှန်ပြသခြင်းများအတွက် အသုံးပြုကြပါသည်။ Equidistant projection ၏ဥပမာများမှာ Plate Carree Equidistant Cylindrical ( Fig. 8.19 တွင်ကြည့်ပါ) နှင့် Equirectangular projection တို့ဖြစ်ကြပါသည်။ ကမ္ဘာ့ကုလသမဂ္ဂ သင်္ကေတအတွက် အသုံးပြုထားသော projection မှာ Azimuthal Equidistant projection ဖြစ်ပါသည် (Fig. 8.20 တွင်ကြည့်ပါ)။

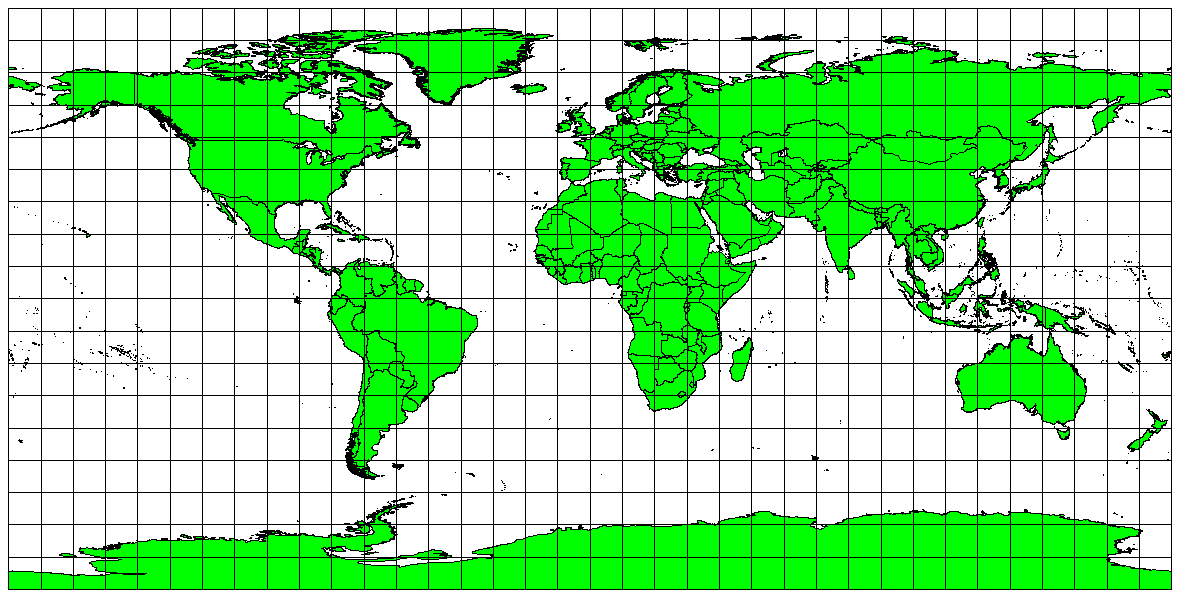
../../_images/plate_carree_projection.png — Fig. 8.19 တိကျသော အကွာအဝေးတိုင်းတာမှုများ အရေးကြီးသည့်ကိစ္စမျိုးတွင် Plate Carree Equidistant Cylindrical projection အား ဥပမာအနေဖြင့် အသုံးပြုထားပါသည်။

../../_images/azimuthal_equidistant_projection.png — Fig. 8.20 ကမ္ဘာ့ကုလသမဂ္ဂ လိုဂိုတွင် Azimuthal Equidistant projection ကိုအသုံးပြုထားပါသည်။

8.4.3. ဧရိယာညီ မြေပုံအရိပ်ချစနစ်များ (Projections with equal areas)

မြေပုံတစ်ခုလုံးပေါ်ရှိ ဧရိယာများသည် ကမ္ဘာမြေပေါ်ရှိ ဧရိယာများနှင့် အချိုးကျ တူညီလျှင် မြေပုံသည် ဧရိယာညီ မြေပုံ တစ်ခုဖြစ်ပါသည်။ ယေဘုယျအကိုးအကားဆိုင်ရာမြေပုံများနှင့် ပညာရေးဆိုင်ရာမြေပုံများတွင် ဧရိယာညီ projection များကိုအသုံးပြုရန် လိုအပ်လေ့ရှိပါသည်။ ဧရိယာနှင့်ပတ်သက်သော တွက်ချက်မှုများကို အသားပေးလုပ်ဆောင်လိုသောအခါ အဆိုပါ မြေပုံများသည် အကောင်းဆုံးဖြစ်ပါသည်။ ဥပမာအားဖြင့် သင့်မြို့ထဲရှိ ဧရိယာတစ်ခုသည် ဈေးအသစ်တစ်ခု ဆောက်လုပ်ရန်အတွက် လုံလောက်သောဧရိယာရှိမရှိကို လေ့လာဆန်းစစ်ရာတွင် ဧရိယာညီ projection များကို အသုံးပြုလျှင် အကောင်းဆုံးဖြစ်ပါသည်။ အခြား‌သော projection များထက် ဧရိယာညီ projection များကို အသုံးပြုပါက ဆန်းစစ်လေ့လာမည့်ဧရိယာကြီးလေလေ တိုင်းတာမှုပိုမိုတိကျလေလေဖြစ်သော်လည်း အခြားတစ်ဘက်တွင် ထောင့်မှန်ကန်မှု မရှိသည်များ ရှိပါမည်။ ဧရိယာအသေးများတွင် ထောင့်မှားယွင်းမှုများ နည်းပါးနိုင်ပါလိမ့်မည်။ Alber’s equal area ၊ Lambert’s equal area နှင့် Mollweide Equal Area Cylindrical projections (Fig. 8.21 တွင်ပြထားသည့်အတိုင်း) များသည် GIS တွင်တွေ့ရလေ့ရှိသော ဧရိယာညီ projection အမျိုးအစားများဖြစ်ကြပါသည်။

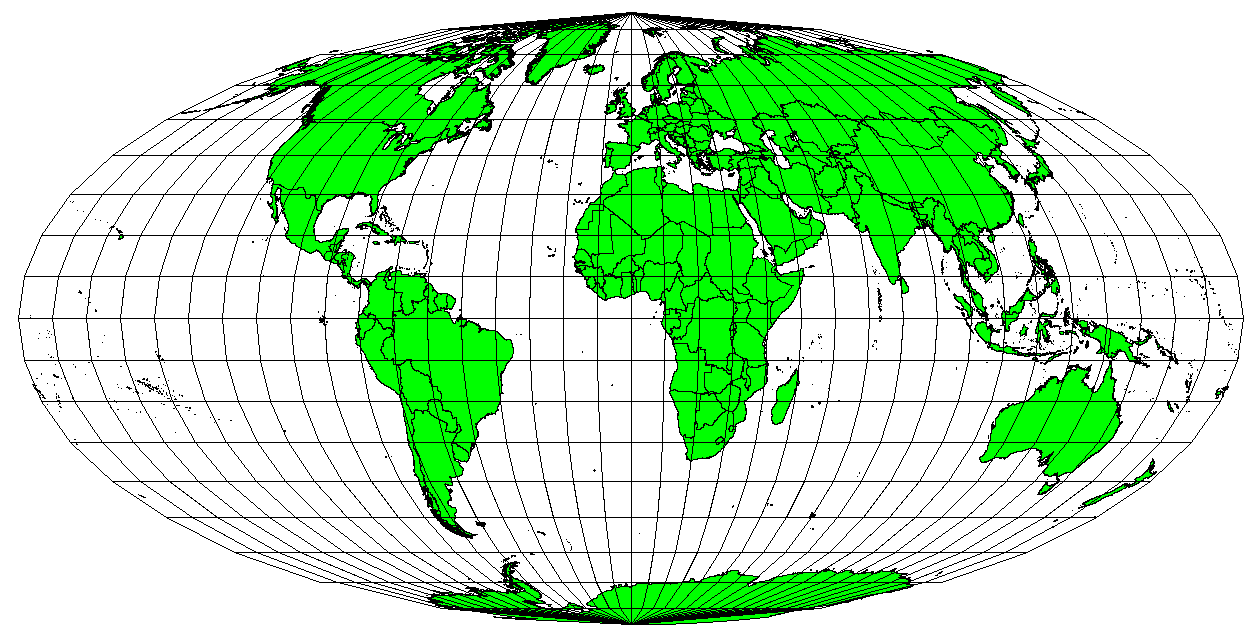
../../_images/mollweide_equal_area_projection.png — Fig. 8.21 မြေပုံဧရိယာများအားလုံးသည် ကမ္ဘာမြေပေါ်ရှိဧရိယာများနှင့် အချိုးကျတူညီစေရန် Mollweide Equal Area Cylindrical projection အား ဥပမာအနေဖြင့် အသုံးပြုထားပါသည်။

Map projection သည် အလွန်ရှုပ်ထွေးသောအကြောင်းအရာတစ်ခုဖြစ်ပါသည်။ ကမ္ဘာတစ်ဝန်း ရာဂဏန်းနှင့်ချီသော projection များစွာရှိပြီး တစ်ခုချင်းစီသည် ကမ္ဘာမြေမျက်နှာပြင်၏ အစိတ်အပိုင်းတစ်ခုခုကို မြေပုံစာရွက်ပေါ်တွင် တတ်နိုင်သမျှ အကောင်းဆုံးဖြစ်အောင် ပုံဖော်နိုင်ရန် လုပ်ဆောင်ထားကြပါသည်။ လက်တွေ့တွင် သင့်ရွေးချယ်မှုပေါ်မူတည်ပြီး အသုံးပြုမည့် projection ကိုရွေးချယ်ရပါလိမ့်မည်။ နိုင်ငံအများစုတွင် အသုံးများသော projection များရှိပြီး data များကို ပြောင်းလဲအသုံးပြုသောအခါ နိုင်ငံအလိုက် သင့်လျော်သည့် projection များကို ပြောင်းလဲအသုံးပြုကြပါသည်။

8.5. ရည်ညွှန်းကိုဩဒိနိတ်စနစ် (CRS) အကြောင်းအသေးစိတ် (Coordinate Reference System (CRS) in detail)

ရည်ညွှန်းကိုဩဒိနိတ်စနစ် (CRS) များကြောင့် ကမ္ဘာပေါ်ရှိ နေရာတိုင်းကို ကိုဩဒိနိတ်ဟုခေါ်သော ဂဏန်း ၃ ခုဖြင့် သတ်မှတ်နိုင်ပါသည်။ ယေဘုယျအားဖြင့် CRS ကို projected coordinate reference systems (Cartesian သို့မဟုတ် rectangular coordinate reference systems ဟုလည်း ခေါ်ဆိုပါသည်) နှင့် geographic coordinate reference systems ဟူ၍ ခွဲခြားနိုင်ပါသည်။

8.5.1. Geographic Coordinate Systems

Geographic Coordinate Reference Systems ကို အလွန်အသုံးများကြပါသည်။ ကမ္ဘာမြေပေါ်ရှိ တည်နေရာတစ်ခုကို ဖော်ပြရန် လတ္တီကျုနှင့် လောင်ဂျီကျု ဒီဂရီတန်ဖိုးများကိုအသုံးပြုကြပြီး တစ်ခါတရံတွင် အမြင့်တန်ဖိုးကိုလည်း အသုံးပြုကြပါသည်။ အသုံးအများဆုံးတစ်ခုမှာ WGS 84 ဖြစ်ပါသည်။

လတ္တီကျူမျဉ်းများ သည် အီကွေတာနှင့်အပြိုင်ရှိနေပြီး ကမ္ဘာကြီး၏ မြောက်မှတောင် (သို့မဟုတ် တောင်မှမြောက်သို့) ၁၈၀ ဒီဂရီထိ အပိုင်းညီ ပိုင်းခြားထားပါသည်။ လတ္တီကျုမျဉ်းအတွက် စမှတ်မျဉ်းသည် အီကွေတာဖြစ်ပြီး ကမ္ဘာတစ်ခြမ်းစီ ကို အပိုင်း ၉၀ စီ ပိုင်းခြားထားပါသည်၊ တစ်ပိုင်းချင်းစီသည် တစ် ဒီဂရီ ဖြစ်ပါသည်။ မြောက်ကမ္ဘာခြမ်းတွင် လတ္တီကျုမျဉ်းကို အီကွေတာ 0 ဒီဂရီမှစတင်ပြီး မြောက်ဝင်ရိုးစွန်းအထိ ၉၀ ဒီဂရီတိုင်းတာပါသည်။ တောင်ကမ္ဘာခြမ်းတွင် လတ္တီကျုမျဉ်းကို အီကွေတာ 0 ဒီဂရီမှစတင်ပြီး တောင်ဝင်ရိုးစွန်းအထိ ၉၀ ဒီဂရီတိုင်းတာပါသည်။ မြေပုံများအား digitise ပြုလုပ်ရာတွင် ရိုးရှင်းစေရန် တောင်ကမ္ဘာခြမ်းရှိ လတ္တီကျုဒီဂရီများကို အနုတ် တန်ဖိုး (0 မှ -90 ဒီဂရီအထိ) သတ်မှတ်လေ့ရှိပါသည်။ ကမ္ဘာပေါ်ရှိ လတ္တီကျုမျဉ်းများအကြားအကွာအဝေးသည် အတူတူပင်ဖြစ်ပါသည် (၆၀ ရေမိုင်)။ Fig. 8.22 တွင်ကြည့်ပါ။

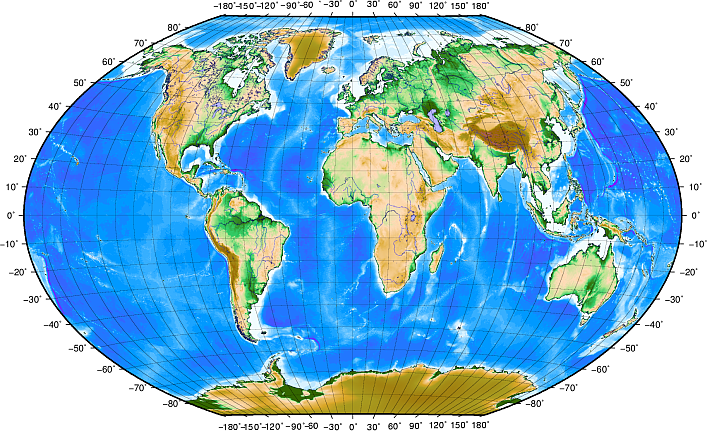
../../_images/geographic_crs.png — Fig. 8.22 အီကွေတာနှင့်အပြိုင် လတ္တီကျုမျဉ်းများနှင့် Greenwich ကိုဖြတ်သွားသော prime meridian နှင့်အပြိုင် လောင်ဂျီကျုမျဉ်းများရှိသော Geographic coordinate system

လောင်ဂျီကျုမျဉ်း များသည် တစ်သမတ်တည်းရှိမနေပါ။ လောင်ဂျီကျုမျဉ်းများသည် အီကွေတာနှင့် ထောင့်မှန်အနေအထားဖြစ်နေပြီး ဝင်ရိုးစွန်းများတွင် သွားစုဆုံကြပါသည်။ လောင်ဂျီကျုမျဉ်းများအတွက် စမှတ် (prime meridian) သည် Greenwich (အင်္ဂလန်) ကိုဖြတ်ပြီး မြောက်ဝင်ရိုးစွန်းမှ တောင်ဝင်ရိုးစွန်းသို့ ချိတ်ဆက်ပါသည်။ လောင်ဂျီကျုမျဉ်းများအား prime meridian ၏ 0 မှ 180 ဒီဂရီ အရှေ့ဘက် သို့မဟုတ် အနောက်ဘက်သို့ တိုင်းတာပါသည်။ Prime meridian ၏ အနောက်ဘက်သို့ တိုင်းတာသော တန်ဖိုးများကို ဒီဂျစ်တယ်မြေပုံရေးဆွဲခြင်း application များတွင် အနုတ် တန်ဖိုးများဖြင့် သတ်မှတ်သည်ကို မှတ်သားထားပါ။ Fig. 8.22 တွင်ကြည့်ပါ။

အီကွေတာတွင် လောင်ဂျီကျုမျဉ်းတစ်ကြောင်းမှ ဖော်ပြသောအကွာအဝေးသည် လတ္တီကျု တစ် ဒီဂရီမှ ဖော်ပြသောအကွာအဝေးနှင့် အတူတူဖြစ်ပါသည်။ ဝင်ရိုးစွန်းဘက်သို့ ရွေ့သွားတိုင်း လောင်ဂျီကျုမျဉ်းများအကြား အကွာအဝေးသည် တရွေ့ရွေ့နည်းလာမည်ဖြစ်ပြီး ဝင်ရိုးစွန်းနေရာအတိအကျတွင် လောင်ဂျီကျု ၃၆၀ ဒီဂရီမျဉ်းများအားလုံးကို point တစ်ခုတည်းဖြင့် ပြသမည်ဖြစ်သည်။ Geographic coordinate system အသုံးပြုပါက ကမ္ဘာကြီးကို စတုရန်းကွက်များအဖြစ် ပိုင်းခြားထားသော လိုင်း grid များ ရှိပြီး အီကွေတာ၌ 12363.365 စတုရန်းကီလိုမီတာခန့် လွှမ်းခြုံမည်ဖြစ်ပါသည်။ အဆိုပါ စတုရန်းကွက်အတွင်းရှိ နေရာတစ်နေရာရာကို ဆုံးဖြတ်ရာတွင် များစွာအသုံးမဝင်ပါ။

အမှန်တကယ်အသုံးဝင်စေရန် မြေပုံ grid တစ်ခုကို လုံလောက်သောအပိုင်းငယ်များအဖြစ် ပိုင်းခြားရပါမည်၊ သို့မှသာ မြေပုံပေါ်ရှိ point တစ်ခု၏တည်နေရာကို ဖော်ပြရာတွင် (လက်ခံနိုင်သော တိကျမှုနှင့်အတူ) အသုံးပြုနိုင်မည်ဖြစ်သည်။ ထိုသို့လုပ်ဆောင်ရန် ဒီဂရီများကို မိနစ်များ (') နှင့် စက္ကန့်များ (") အဖြစ်သို့ ပိုင်းခြားပါမည်။ တစ်ဒီဂရီတွင် မိနစ် ၆၀ ရှိပြီး တစ်မိနစ်တွင် စက္ကန့် ၆၀ ရှိပါသည် (တစ်ဒီဂရီတွင် ၃၆၀၀ စက္ကန့်ရှိပါသည်)။ ထို့ကြောင့် အီကွေတာတွင် လတ္တီကျု သို့မဟုတ် လောင်ဂျီကျု တစ် စက္ကန့်သည် 30.87624 မီတာဖြစ်ပါသည်။

8.5.2. Projected coordinate reference systems

အတိုင်းအတာ ၂ ခုပါသော two-dimensional ကိုဩဒိနိတ်ရည်ညွှန်းစနစ်အား ဝင်ရိုး နှစ်ခုဖြင့် သတ်မှတ်ကြပါသည်။ ဝင်ရိုးတစ်ခုနှင့်တစ်ခု ထောင့်မှန်နေရာတွင် XY-plane (Fig. 8.23 ရှိ ဘယ်ဘက်ပုံကိုကြည့်ပါ) တစ်ခုရှိပါသည်။ ရေပြင်ညီဝင်ရိုးကို ပုံမှန်အားဖြင့် X ဟုခေါ်ဆိုပြီး ဒေါင်လိုက်ဝင်ရိုးကို Y ဟုခေါ်ဆိုပါသည်။ အတိုင်းအတာ ၃ ခုပါသော three-dimensional ကိုဩဒိနိတ်ရည်ညွှန်းစနစ်တွင် Z ဟုခေါ်သောအခြားဝင်ရိုးတစ်ခုပါရှိပါသည်။ ၎င်းသည်လည်း X နှင့် Y ဝင်ရိုးများနှင့် ထောင့်မှန်ကျပါသည်။ Z ဝင်ရိုးသည် တတိယအတိုင်းအတာဖြစ်ပါသည် (Fig. 8.23 ရှိ ညာဘက်ပုံကိုကြည့်ပါ)။ Spherical ကိုဩဒိနိတ်များဖြင့် ဖော်ပြထားသော point တိုင်းကို X Y Z ကိုဩဒိနိတ်အနေဖြင့် ဖော်ပြပေးနိုင်ပါသည်။

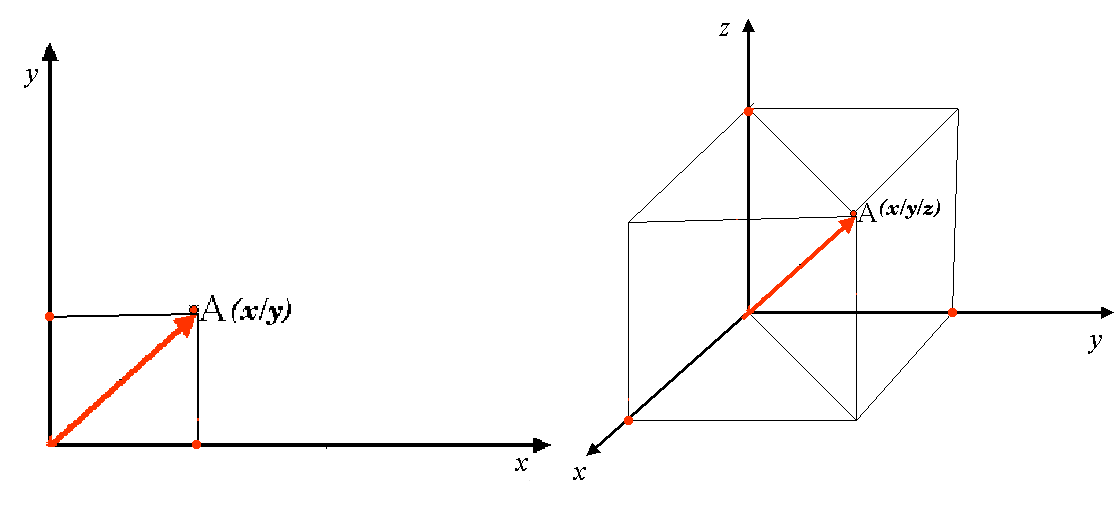
../../_images/projected_crs.png — Fig. 8.23 အတိုင်းအတာ ၂ ခုပါသော နှင့် အတိုင်းအတာ ၃ ခုပါသော ကိုဩဒိနိတ်ရည်ညွှန်းစနစ်

ကမ္ဘာ့တောင်ဘက်ခြမ်း (အီကွေတာ၏တောင်ဘက်) ရှိ projected coordinate system တစ်ခုသည် ပုံမှန်အားဖြင့် အီကွေတာပေါ်ရှိ သီးခြား လောင်ဂျီကျု တစ်ခုတွင် အစပြုပါသည်။ ဆိုလိုသည်မှာ Y-တန်ဖိုးများသည် တောင်ဘက်သို့သွားလေလေ တန်ဖိုးမြင့်လေလေ ဖြစ်ပြီး X-တန်ဖိုးများသည် အနောက်ဘက်သို့သွားလေလေ တန်ဖိုးမြင့်လေလေဖြစ်ပါသည်။ ကမ္ဘာ့မြောက်ဘက်ခြမ်း (အီကွေတာ၏မြောက်ဘက်) တွင်လည်း အီကွေတာပေါ်ရှိ သီးခြား လောင်ဂျီကျု တစ်ခုတွင် အစပြုပါသည်။ သို့သော် Y-တန်ဖိုးများသည် မြောက်ဘက်သို့သွားလေလေ တန်ဖိုးမြင့်လေလေဖြစ်ပြီး X-တန်ဖိုးများသည် အရှေ့ဘက်သို့သွားလေလေ တန်ဖိုးမြင့်လေလေဖြစ်ပါသည်။ နောက်လာမည့်အပိုင်းတွင် တောင်အာဖရိကအတွက် အသုံးပြုလေ့ရှိသော Universal Transverse Mercator (UTM) ဟုခေါ်သည့် projected coordinate reference system အကြောင်း ဖော်ပြသွားပါမည်။

8.6. Universal Transverse Mercator (UTM) CRS အကြောင်း အသေးစိတ် (Universal Transverse Mercator (UTM) CRS in detail)

Universal Transverse Mercator (UTM) coordinate reference system သည် အီကွေတာပေါ်ရှိ သီးခြား လောင်ဂျီကျု တစ်ခုတွင် အစပြုပါသည်။ Y-တန်ဖိုးများသည် တောင်ဘက်သို့သွားလေလေ တန်ဖိုးမြင့်လေလေဖြစ်ပြီး X-တန်ဖိုးများသည် အနောက်ဘက်သို့သွားလေလေ တန်ဖိုးမြင့်လေလေဖြစ်သည်။ UTM CRS သည် ကမ္ဘာလုံးသုံး မြေပုံအရိပ်ချစနစ်တစ်ခုဖြစ်ပါသည်။ ဆိုလိုသည်မှာ ၎င်းကို တစ်ကမ္ဘာလုံးတွင် ယေဘုယျအားဖြင့် အသုံးပြုကြပါသည်။ သို့သော် ‘map projection များ၏တိကျမှု’ ဆိုသည့်အပိုင်းတွင် ဖော်ပြခဲ့သည့်အတိုင်း ဧရိယာကြီးလေလေ (ဥပမာ တောင်အာဖရိက) ထောင့်မှန်ကန်မှု distortion ၊ အကွာအဝေး distortion နှင့် ဧရိယာ distortion များလေလေဖြစ်ပါသည်။ Distortion များစွာမဖြစ်စေရန်အတွက် ကမ္ဘာကြီးအား ဇုန် ၆၀ ခု ပိုင်းခြားထားပြီး တစ်ခုနှင့်တစ်ခုကြား အရှေ့မှအနောက်သို့ ၆ ဒီဂရီ လောင်ဂျီကျုစီ ကျယ်ပါသည်။ UTM zones များကို ဂဏန်း ၁ မှ ၆၀ အထိနံပါတ်တပ်ထားပြီး antimeridian (အနောက်ဘက် ၁၈၀ ဒီဂရီ လောင်ဂျီကျု၌ရှိသော zone 1) မှ အစပြုပါသည်၊ ထို့နောက် Fig. 8.24 တွင် ပြထားသည့်အတိုင်း antemeridian မှအရှေ့ဘက်သို့ (အရှေ့ဘက် ၁၈၀ လောင်ဂျီကျု၌ရှိသော zone 60) ဆက်တိုးလာပါသည်။

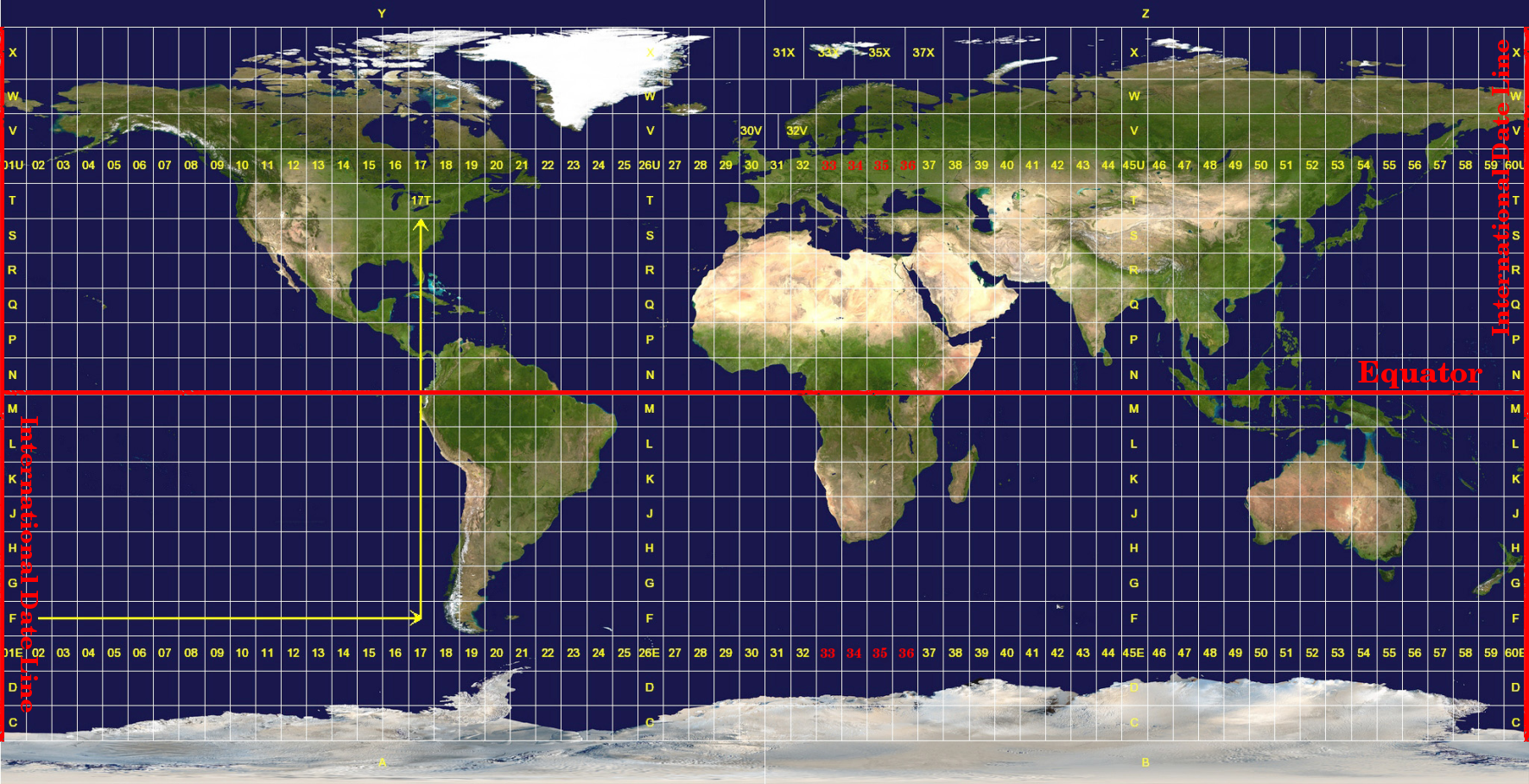
../../_images/utm_zones.png — Fig. 8.24 Universal Transverse Mercator ဇုန်များ။ တောင်အာဖရိကအတွက် UTM zones 33S ၊ 34S ၊ 35S ၊ နှင့် 36S တို့ကို အသုံးပြုပါသည်။

Fig. 8.24 နှင့် Fig. 8.25 တွင် မြင်တွေ့ရသည့်အတိုင်း distortion နည်းစေရန် တောင်အာဖရိကအား UTM zone ၄ ခုဖြင့် လွှမ်းခြုံထားပါသည်။ Zone များကို UTM 33S ၊ UTM 34S ၊ UTM 35S နှင့် UTM 36S ဟုခေါ်ဆိုကြပါသည်။ Zone ၏နောက်ရှိ S စာလုံးသည် အီကွေတာ၏ တောင်ဘက် တွင် UTM zone များတည်ရှိသည်ကို ဆိုလိုပါသည်။

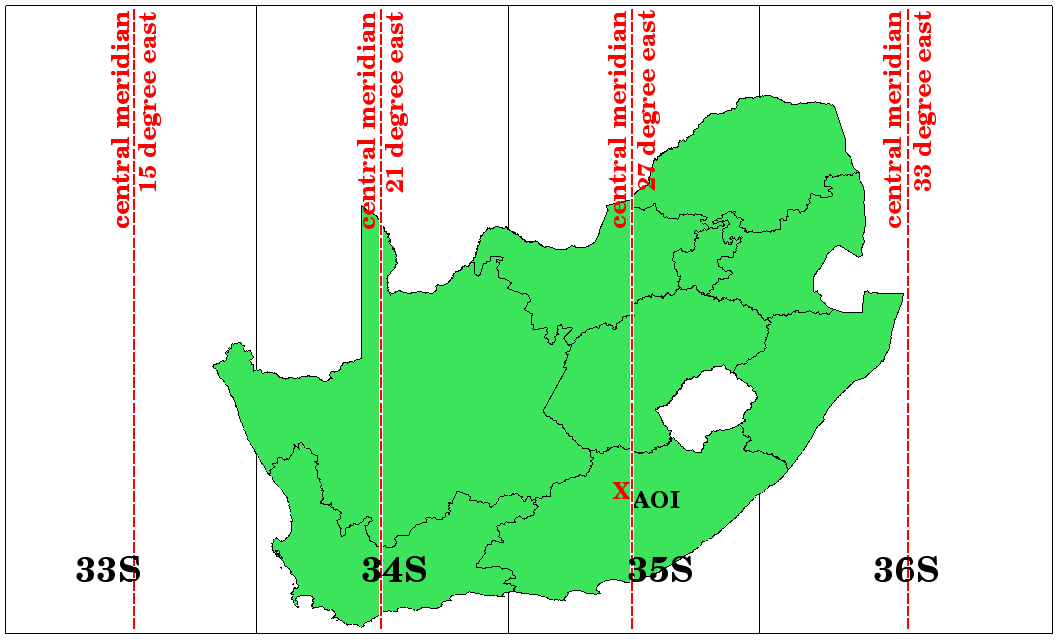
../../_images/utm_for_sa.png — Fig. 8.25 တောင်အာဖရိကအတွက် တိကျမှုကောင်းကောင်းဖြင့် အရိပ်ချရာတွင် အသုံးပြုသော UTM zones 33S ၊ 34S ၊ 35S ၊ နှင့် 36S ။ အနီရောင် ကြက်ခြေခတ်သည် Area of Interest (AOI) ကိုပြသပါသည်။

ဥပမာအားဖြင့် Fig. 8.25 တွင် အနီရောင်ကြက်ခြေခတ်ဖြင့်ပြထားသော Area of Interest (AOI) အတွင်းတွင် two-dimensional ကိုဩဒိနိတ်တစ်ခု သတ်မှတ်လိုသည်ဆိုပါစို့။ ဧရိယာသည် UTM zone 35S အတွင်းတွင် ကျရောက်နေသည်ကို မြင်တွေ့နိုင်ပါသည်။ ဆိုလိုသည်မှာ distortion နည်းစေရန်နှင့် ဆန်းစစ်လေ့လာမှုရလာဒ်များ တိကျစေရန်အတွက် UTM zone 35S ကို coordinate reference system အနေဖြင့်အသုံးပြုသင့်ပါသည်။

တည်နေရာတစ်ခု၏ ကိုဩဒိနိတ်ကို UTM ဖြင့်ဖော်ပြရာတွင် zone နံပါတ် (35) နှင့်အတူ မြောက်ဘက်-northing (Y) တန်ဖိုး နှင့် အရှေ့ဘက်-easting (X) တန်ဖိုး များကို မီတာဖြင့် ဖော်ညွှန်းပေးရပါမည်။ မြောက်ဘက် တန်ဖိုး သည် အီကွေတာမှ တည်နေရာနှင့် ကွာဝေးသော မီတာအကွာအဝေးဖြစ်ပါသည်။ အရှေ့ဘက်တန်ဖိုး သည် အသုံးပြုထားသော UTM zone ၏ central meridian (လောင်ဂျီကျု) မှ တည်နေရာနှင့် ကွာဝေးသော မီတာအကွာအဝေးဖြစ်ပါသည်။ UTM zone 35S အတွက်ဆိုလျှင် Fig. 8.25 တွင်ပြထားသည့်အတိုင်း 27 degrees East ဖြစ်ပါမည်။ ထို့အပြင် အီကွေတာ၏တောင်ဘက်အခြမ်းကို အသုံးပြုနေသောကြောင့် UTM coordinate reference system တွင် အနုတ်တန်ဖိုးများကို ခွင့်မပြုပါ၊ northing (Y) တန်ဖိုးတွင် 10,000,000 မီတာ false northing value တစ်ခုနှင့် easting (X) တန်ဖိုးတွင် 500,000 မီတာ false easting value တစ်ခုကို ထည့်သွင်းပေးရပါမည်။ Area of Interest အတွက် UTM 35S ကိုဩဒိနိတ်အမှန်ကို ရှာဖွေနည်းကို ဥပမာအနေဖြင့် ပြသပေးပါမည်။

8.6.1. မြောက်ဘက် (Y) တန်ဖိုး (The northing (Y) value)

ကျွန်ုပ်တို့ရှာဖွေလိုသောနေရာသည် အီကွေတာ၏တောင်ဘက် 3,550,000 မီတာဖြစ်သောကြောင့် northing (Y) တန်ဖိုးတွင် အနုတ်လက္ခဏာ ထည့်သွင်းပေးပါ၊ -3,550,000 မီတာဖြစ်သွားပါမည်။ UTM ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်များအရ false northing value 10,000,000 မီတာကို ပေါင်းပေးရပါမည်။ ထို့ကြောင့် ကိုဩဒိနိတ်၏ northing (Y) တန်ဖိုးသည် 6,450,000 မီတာဖြစ်သွားပါမည် (-3,550,000 မီတာ + 10,000,000 မီတာ)။

8.6.2. အရှေ့ဘက် (X) တန်ဖိုး (The easting (X) value)

ပထမဦးစွာ UTM zone 35S အတွက် central meridian (လောင်ဂျီကျု) ကိုရှာဖွေရပါမည်။ Fig. 8.25 တွင်တွေ့ရသည့်အတိုင်း ၎င်းသည် 27 degrees East ဖြစ်ပါသည်။ ကျွန်ုပ်တို့ရှာဖွေနေသည့်နေရာသည် central meridian မှ အနောက်ဘက် မီတာ 85,000 ဖြစ်ပါသည်။ Northing တန်ဖိုးလိုပင် easting (X) တန်ဖိုးတွင်လည်း အနုတ် လက္ခဏာထည့်ပေးပါ၊ -85,000 မီတာ ဖြစ်သွားပါမည်။ UTM အဓိပ္ပါယ်ဖွင့်ဆိုချက်များအရ false easting value 500,000 မီတာကို ပေါင်းပေးရပါမည်။ ထို့ကြောင့် ကိုဩဒိနိတ်၏ easting (X) တန်ဖိုးသည် 415,000 မီတာ (-85,000 မီတာ + 500,000 မီတာ) ဖြစ်သွားပါမည်။ နောက်ဆုံးတွင် zone နံပါတ် ကို easting တန်ဖိုးရှေ့တွင် ထည့်ပေးရပါမည်။

ရလာဒ်အနေဖြင့် ကျွန်ုပ်တို့စိတ်ဝင်စားသည့် Point of Interest အတွက် ကိုဩဒိနိတ်သည် UTM zone 35S ဖြင့်အရိပ်ချထားပြီး 35 415,000 m E / 6,450,000 m N ဟုဖော်ပြပေးမည်ဖြစ်ပါသည်။ အချို့ GIS software များတွင် UTM zone 35S အမှန်ကို သတ်မှတ်သောအခါ ကွန်ပျူတာစနစ်အတွင်း ယူနစ်ကို မီတာဖြင့်သတ်မှတ်ပေးပါသည်၊ ကိုဩဒိနိတ် ကိုလည်း 415,000 6,450,000 ဟူ၍ ရိုးရိုးရှင်းရှင်း ဖော်ပြပေးပါသည်။

8.7. On-The-Fly Projection

GIS ထဲတွင် သင်အသုံးပြုလိုသော data များသည် အခြားမတူညီသည့် coordinate reference system များဖြင့် ဖြစ်နေသည့်အခြေအနေမျိုး ကြုံတွေ့ရနိုင်ပါသည်။ ဥပမာ- UTM 35S projection ဖြင့် တောင်အာဖရိက၏နယ်နိမိတ် vector layer တစ်ခုရှိပြီး မိုးရေချိန်အချက်အလက်များပါသော point vector layer တစ်ခုကို geographic coordinate system WGS84 ဖြင့်ရှိသည် ဆိုကြပါစို့။ GIS ထဲတွင် အဆိုပါ layer နှစ်ခုသည် projection မတူညီသည့်အတွက်ကြောင့် တစ်နေရာစီ ဖြစ်နေပါမည်။

ထိုပြဿနာကို ဖြေရှင်းရန် GIS software များစွာတွင် on-the-fly projection ဟုခေါ်သော လုပ်ဆောင်ချက်တစ်ခုပါရှိပါသည်။ ၎င်းသည် GIS ကိုစတင်သုံးစွဲသောအခါ projection တစ်ခုကို သတ်မှတ် ပေးနိုင်ပြီး ထည့်သွင်းလိုက်သော layer များအားလုံးကို သင်သတ်မှတ်ပေးထားသော projection ဖြင့် အလိုအလျောက်ပြသပေးမည်ဖြစ်သည်။ ထိုလုပ်ဆောင်ချက်ဖြင့် coordinate reference system မတူညီသော layer များကို GIS ၏မြေပုံမြင်ကွင်းအတွင်း ပြသပေးနိုင်ပါမည်။ QGIS ထဲတွင် အဆိုပါလုပ်ဆောင်ချက်ကို default အနေဖြင့်လုပ်ဆောင်ပေးပါသည်။

8.8. အဖြစ်များသောပြဿနာများ/သတိထားရမည့်အရာများ (Common problems / things to be aware of)

မြေပုံအရိပ်ချခြင်း ခေါင်းစဉ်သည် အလွန်ရှုပ်ထွေးပြီး ပထဝီဝင်ပညာရပ်ကျွမ်းကျင်သူများ သို့မဟုတ် အခြားသော GIS ကျွမ်းကျင်သူများပင်လျှင် map projection များနှင့် coordinate reference system များ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်အမှန်နှင့်ပတ်သက်ပြီး ပြဿနာများကြုံတွေ့ရလေ့ရှိပါသည်။ များသောအားဖြင့် GIS တွင်လုပ်ဆောင်သောအခါ projection ပြောင်းထားသော data များရှိနေပြီးသားဖြစ်ပါသည်။ အများစုကိစ္စရပ်များတွင် အဆိုပါ data များသည် CRS တစ်ခုခုထဲတွင် ရှိနေမည်ဖြစ်သည်၊ ထို့ကြောင့် CRS အသစ်တစ်ခုဖန်တီးရန် မလိုအပ်ပါသလို CRS တစ်ခုမှ အခြားတစ်ခုသို့ ပြောင်းလဲရန်ပင် မလိုအပ်ပါ။ Map projection နှင့် CRS များ၏ အဓိပ္ပါယ်ဆိုလိုရင်းကို သိရှိထားပါက အမြဲတမ်းအသုံးဝင်နေမည်ဖြစ်သည်။

8.9. လေ့လာခဲ့ပြီးသည့်အရာများ (What have we learned?)

ဤစာမျက်နှာတွင် ဖော်ပြခဲ့သည်တို့ကို အကျဉ်းချုပ်ဆိုရသော်-

Map projection များသည် ကမ္ဘာမြေမျက်နှာပြင်အား စာရွက်တစ်ရွက် သို့မဟုတ် ကွန်ပျုတာဖန်သားပေါ်တွင် ပုံဖော်ခြင်းဖြစ်သည်။
ကမ္ဘာလုံးသုံး map projection များရှိပါသည်၊ သို့သော် map projection အများစုကို ကမ္ဘာမြေမျက်နှာပြင်၏ ဧရိယာငယ်များ အတွက် အကောင်းဆုံးဖြစ်စေရန် ဖန်တီးထားကြပါသည်။
Map projection များသည် လုံးဝန်းသောကမ္ဘာကြီးကို လုံးဝ အတိအကျ ပုံဖော်ပြသနိုင်ခြင်း မရှိပါ။ ထောင့်မှန်ကန်မှု၊ အကွာအဝေးမှန်ကန်မှု နှင့် ဧရိယာမှန်ကန်မှုဆိုင်ရာ distortion များရှိကြပါသည်။ Map projection တစ်ခုထဲတွင် အဆိုပါအားလုံး မှန်ကန်စေရန်မှာ မဖြစ်နိုင်ပါ။
Coordinate reference system (CRS) သည် ကမ္ဘာမြေပေါ်ရှိ လက်တွေ့တည်နေရာများနှင့် မြေပုံများ ဆက်စပ်ပုံကို သတ်မှတ်ပေးပါသည်။
Coordinate reference system (CRS) နှစ်မျိုးရှိပါသည်- Geographic Coordinate Systems နှင့် Projected Coordinate Systems တို့ဖြစ်ကြပါသည်။
On the Fly projection ဆိုသည်မှာ GIS ထဲရှိ လုပ်ဆောင်မှုတစ်ခုဖြစ်ပြီး coordinate reference system မတူညီသော layer များကို ထပ် (overlay) ပြီး ကြည့်ရှုနိုင်ပါသည်။

8.10. ယခု သင်တို့ ကြိုးစားကြည့်ပါ! (Now you try!)

အောက်ပါတို့မှာ သင်တန်းသားများအား ကြိုးစားကြည့်စေရန် အချက်တစ်ချို့ဖြစ်ပါသည်-

QGIS ကိုဖွင့်ပါ
Project ► Properties… ► CRS ထဲတွင် No projection (or unknown/non-Earth projection) ကိုအမှန်ခြစ်ပါ
ဧရိယာတူညီသော်လည်း projection မတူညီသော layer နှစ်ခုကို ထည့်သွင်းပါ
Layer နှစ်ခုပေါ်တွင် နေရာအတော်များများ၏ ကိုဩဒိနိတ်များကို သင်တန်းသားများအား ရှာဖွေစေပါ။ Layer နှစ်ခုအား ထပ် (overlay) ရန် မဖြစ်နိုင်ကြောင်း သင်တန်းသားများအား ပြသပါ။
ထို့နောက် Project Properties dialog ထဲတွင် coordinate reference system ကို Geographic/WGS 84 အဖြစ်သတ်မှတ်ပါ
အဆိုပါ layer နှစ်ခုကို ထပ်မံ၍ ထည့်သွင်းပြီး project အတွက် CRS တစ်ခုသတ်မှတ်ပုံအား သင်တန်းသားများအား ပြသပါ (“on-the-fly” projection ကိုဖွင့်ပေးခြင်း)
QGIS ထဲတွင် Project Properties dialog ကိုဖွင့်ပြီး မတူညီသည့် Coordinate Reference System များစွာရှိကြောင်းကို သင်တန်းသားများအား ပြသပေးပါ။ Layer တစ်မျိုးတည်းကို အမျိုးမျိုးသော CRS များပြောင်းလဲ၍ သင်တန်းသားများအား ပြသပေးနိုင်ပါသည်။

8.11. စဉ်းစားရမည့်အချက် (Something to think about)

သင့်တွင် ကွန်ပျူတာမရှိလျှင်လည်း မြေပုံအရိပ်ချခြင်း အုပ်စု ၃ မျိုး၏ နိယာမများကို သင်တန်းသားများအား ပြသပေးနိုင်ပါသည်။ ကမ္ဘာလုံးတစ်ခုနှင့် စာရွက်တစ်ခုကို ယူပြီး စလင်ဒါပုံ၊ ကတော့ချွန်ပုံ နှင့် ပြင်ညီ projection များအကြောင်းကို အကြမ်းဖျဉ်း နမူနာပြသပေးနိုင်ပါသည်။ စာရွက်အကြည်တစ်ခုဖြင့် အတိုင်းအတာ ၂ ခုရှိသော two-dimensional coordinate reference system တစ်ခုတွင် X ဝင်ရိုး နှင့် Y ဝင်ရိုးများကို ဆွဲပြပေးနိုင်ပါသည်။ ထို့နောက် သင်တန်းသားများအား နေရာအသီးသီးအတွက် ကိုဩဒိနိတ်များ (X နှင့် Y တန်ဖိုးများ) ကိုသတ်မှတ်စေပါ။

8.12. နောက်ထပ်ဖတ်ရှုရမည်များ (Further reading)

စာအုပ်များ:

Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

Websites:

QGIS ထဲတွင် map projection များဖြင့်လုပ်ဆောင်ခြင်းအပိုင်းကို QGIS အသုံးပြုသူလမ်းညွှန်ထဲတွင် အသေးစိတ်ဖော်ပြထားပါသည်။

8.13. နောက်ထပ်ဘာအကြောင်းအရာလဲ (What’s next?)

နောက်လာမည့်အခန်းတွင် Map Production (မြေပုံထုတ်လုပ်ခြင်း) အကြောင်း အသေးစိတ်လေ့လာသွားမည်ဖြစ်ပါသည်။