11. တည်နေရာဆိုင်ရာ ဆန်းစစ်လေ့လာခြင်း (သွယ်ဝိုက်တွက်ချက်ခြင်း) (Spatial Analysis (Interpolation))

	ရည်ရွယ်ချက်များ	Spatial analysis ၏တစ်စိတ်တစ်ပိုင်းအနေဖြင့် interpolation ကို နားလည်စေရန်။
	Keyword များ	Point data ၊ interpolation method ၊ Inverse Distance Weighted ၊ Triangulated Irregular Network

11.1. အကျဉ်းချုပ် (Overview)

Spatial analysis သည် မူရင်း data များမှ အချက်အလက်အသစ်များနှင့် အဓိပ္ပါယ်အသစ်များ ဆွဲထုတ်ယူရန်အတွက် spatial အချက်အလက်များကို ကိုင်တွယ်သော လုပ်ငန်းစဉ်ဖြစ်ပါသည်။ များသောအားဖြင့် spatial analysis ကို Geographic Information System (GIS) ဖြင့်လုပ်ဆောင်ပါသည်။ GIS တွင် feature statistics များတွက်ချက်ရန်နှင့် data interpolation ကဲ့သို့သော geoprocessing လုပ်ဆောင်မှုများကိုဆောင်ရွက်ရန် spatial analysis tool များပါရှိပါသည်။ Hydrology (ဇလဗေဒ) နှင့်ပတ်သက်သူများသည် terrain (မြေမျက်နှာသွင်ပြင်) analysis နှင့် hydrological modelling (ကမ္ဘာမြေပေါ်နှင့် အထဲရှိ ရေရွှေ့လျားမှုကို model ပြုလုပ်ခြင်း) ၏အရေးပါမှုကို အာရုံထားပါလိမ့်မည်။ သားငှက်တိရစ္ဆာန်စီမံခန့်ခွဲရေးဆိုင်ရာ လုပ်ဆောင်သူများသည် သားငှက်တိရစ္ဆာန်များ၏တည်နေရာများနှင့် ပတ်ဝန်းကျင်နှင့်၎င်းတို့၏ဆက်နွယ်မှုဆိုင်ရာ ဆန်းစစ်လေ့လာမှု function များကို စိတ်ဝင်စားမည်ဖြစ်သည်။ အသုံးပြုသူတစ်ဦးချင်းစီတွင် လုပ်ဆောင်ရသည့်အလုပ်အမျိုးအစားပေါ်မူတည်၍ စိတ်ဝင်စားသော အရာများကွဲပြားပါလိမ့်မည်။

11.2. Spatial interpolation အကြောင်းအသေးစိတ် (Spatial interpolation in detail)

Spatial interpolation သည် တန်ဖိုးသိပြီးသား point များကို အသုံးပြု၍ အခြားမသိရသေးသော point များရှိ တန်ဖိုးများကို ခန့်မှန်းသည့် လုပ်ငန်းစဉ်ဖြစ်ပါသည်။ ဥပမာ- သင့်နိုင်ငံအတွက် မိုးရွာသွန်းမှု (မိုးရေချိန်) မြေပုံတစ်ခုဖန်တီးရန် တစ်နိုင်ငံလုံးကို လွှမ်းခြုံသော မိုးလေဝသစခန်းများ ညီမျှစွာပြန့်နှံ တည်ရှိနေမည်မဟုတ်ပါ။ Spatial interpolation သည် အနီးအနားရှိ မိုးလေဝသစခန်းများမှ အပူချိန်တိုင်းတာမှုများကိုအသုံးပြုပြီး မှတ်တမ်း data မရှိသေးသော နေရာများရှိ အပူချိန်များကို ခန့်မှန်းပေးနိုင်ပါသည် (Fig. 11.37 တွင်ကြည့်ပါ)။ ထိုသို့သော interpolate ပြုလုပ်ထားသော မျက်နှာပြင်အမျိုးအစားကို statistical surface ဟုခေါ်ဆိုလေ့ရှိပါသည်။ မြေမျက်နှာပြင်အနိမ့်အမြင့် data၊ မိုးရွှာသွန်းမှု၊ နှင်းစုပုံမှု နှင့် လူဦးရေသိပ်သည်းမှု စသည်တို့သည် interpolation အသုံးပြုပြီးတွက်ချက်နိုင်သော အခြား data အမျိုးအစားများဖြစ်ပါသည်။

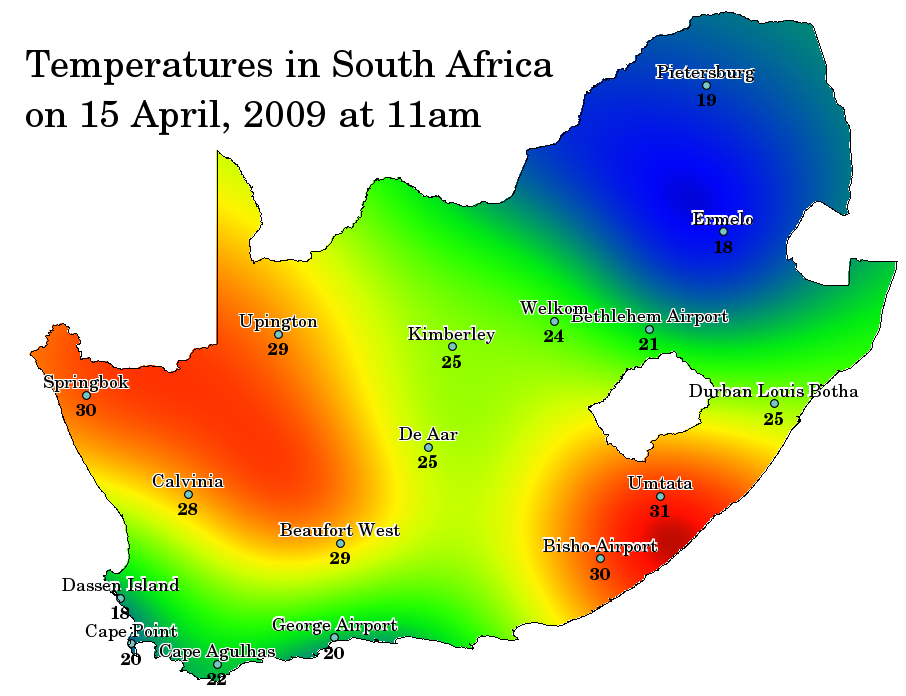
Fig. 11.37 တောင်အာဖရိက မိုးလေဝသစခန်းများမှ interpolate လုပ်ထားသော အပူချိန်ပြမြေပုံ

ကုန်ကျစရိတ်များပြားခြင်းနှင့် အရင်းအမြစ်အကန့်အသတ်များကြောင့် data ကောက်ယူခြင်းကို ရွေးချယ်ကန့်သတ်ထားသော point တည်နေရာများတွင်သာ များသောအားဖြင့် လုပ်ဆောင်ရပါသည်။ GIS တွင် ထို point များကို interpolation ပြုလုပ်ပြီး raster cell များအားလုံးအတွက် ခန့်မှန်းတန်ဖိုးများပါရှိသော raster surface တစ်ခုကို ဖန်တီးနိုင်ပါသည်။

တစ်ဆက်တစပ်တည်းပြသောမြေပုံတစ်ခု၊ ဥပမာ- GPS ဖြင့်တိုင်းတာခဲ့သော အမြင့် point များမှ digital elevation မြေပုံတစ်ခု ထုတ်ယူရာတွင် တိုင်းတာမှုမလုပ်ဆောင်ခဲ့သော သို့မဟုတ် နမူနာမကောက်ယူခဲ့သော နေရာများရှိ တန်ဖိုးများကို အကောင်းဆုံးခန့်မှန်းရန် သင့်လျော်သော interpolation နည်းလမ်းတစ်ခုကို အသုံးပြုရပါမည်။ Interpolation analysis မှရလာဒ်များကို နောက်ပိုင်းတွင် ဧရိယာတစ်ခုလုံးအတွက် ဆန်းစစ်လေ့လာခြင်းများနှင့် modelling အတွက်အသုံးပြုနိုင်ပါသည်။

Interpolation နည်းလမ်းများစွာရှိပါသည်။ ဤမိတ်ဆက်အပိုင်းတွင် ကျယ်ပြန့်စွာအသုံးများသော Inverse Distance Weighting (IDW) နှင့် Triangulated Irregular Networks (TIN) ဟုခေါ်သည့် interpolation နည်းလမ်းနှစ်မျိုးကို ပြသပေးပါမည်။ အခြားသော interpolation နည်းလမ်းများကို ရှာဖွေလိုပါက ဤခေါင်းစဉ်၏အဆုံးတွင်ရှိသော ‘Further Reading’ (နောက်ထပ်ဖတ်ရှုရမည်များ) ကဏ္ဍတွင် ကြည့်ရှုပါ။

11.3. Inverse Distance Weighted (IDW)

IDW interpolation နည်းလမ်းတွင် interpolation ပြုလုပ်စဉ်အတွင်း နမူနာ point များကို weight (အလေးပေး) ပြုလုပ်ပါသည်၊ သို့မှသာ သင်ဖန်တီးလိုသော မသိသေးသည့် point မှ ဝေးကွာလေလေ နမူနာ point တစ်ခု၏လွှမ်းမိုးမှု လျော့ကျလေလေဖြစ်ပါမည် (Fig. 11.38 တွင်ကြည့်ပါ)။

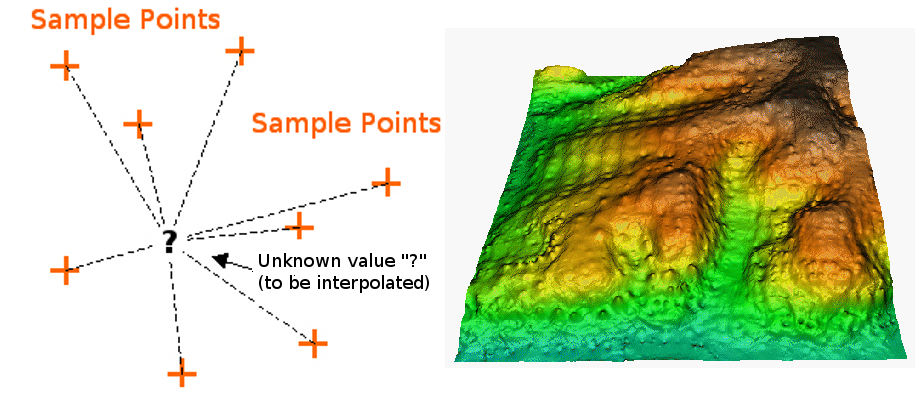
Fig. 11.38 Weight ပြုလုပ်ထားသော နမူနာ point အကွာအဝေးပေါ်အခြေခံထားသော Inverse Distance Weighted interpolation နည်းလမ်း (ဘယ်ဘက်)။ Elevation vector point များမှ interpolate လုပ်ထားသော IDW မျက်နှာပြင် (ညာဘက်)။ ဓာတ်ပုံရင်းမြစ်- Mitas, L., Mitasova, H. (1999)။

Weighting coefficient တစ်ခုကိုအသုံးပြုပြီး နမူနာ point များတွင် weight သတ်မှတ်ပေးပါသည်၊ weighting coefficient သည် point အသစ်မှ အကွာအဝေးတိုးလာလျှင် weight လွှမ်းမိုးမှု မည်သို့လျော့ကျမည်ကို ထိန်းချုပ်ပေးပါသည်။ Interpolation လုပ်ငန်းစဉ်အတွင်း နမူနာ point များသည် မသိသေးသည့် point မှ ဝေးကွာပါက weighting coefficient တန်ဖိုးကြီးလေလေ point များသည်သက်ရောက်မှုနည်းလေလေ ဖြစ်ပါသည်။ Coefficient တန်ဖိုးတိုးလိုက်ပါက မသိသေးသည့် point ၏တန်ဖိုးသည် အနီးဆုံးနမူနာ point ၏တန်ဖိုးကို ချဉ်းကပ်မည်ဖြစ်ပါသည်။

IDW interpolation နည်းလမ်းတွင် အချို့သော အားနည်းချက်များရှိသည်ကိုလည်း သတိထားသင့်ပါသည်- နမူနာ data point များ၏ ပြန့်နှံမှုမညီပါက interpolation ရလာဒ်၏ အရည်အသွေးသည် ကျဆင်းနိုင်ပါသည်။ ထို့အပြင် interpolate ပြုလုပ်ထားသော surface ထဲရှိ အများဆုံးနှင့် အနည်းဆုံး တန်ဖိုးများသည် နမူနာ data point များ၌သာ ဖြစ်ပေါ်နိုင်ပါသည်။ Fig. 11.38 တွင်ပြထားသည့်အတိုင်း နမူနာ data point များပတ်လည်ရှိ တောင်ထိပ်ငယ်များနှင့် ချိုင့်များ အဖြစ် ရလာဒ်ထုတ်ပေးလေ့ရှိပါသည်။

GIS တွင် interpolation ရလာဒ်များကို များသောအားဖြင့် အတိုင်းအတာ ၂ ခုရှိသော (2 dimensional) raster layer တစ်ခုအဖြစ် ပြသပေးပါသည်။ GPS ဖြင့် ကွင်းထဲတွင် ကောက်ယူထားသော အမြင့်နမူနာ point များပေါ်အခြေခံထားသည့် IDW interpolation ရလာဒ်တစ်ခုကို Fig. 11.39 တွင် မြင်တွေ့နိုင်ပါသည်။

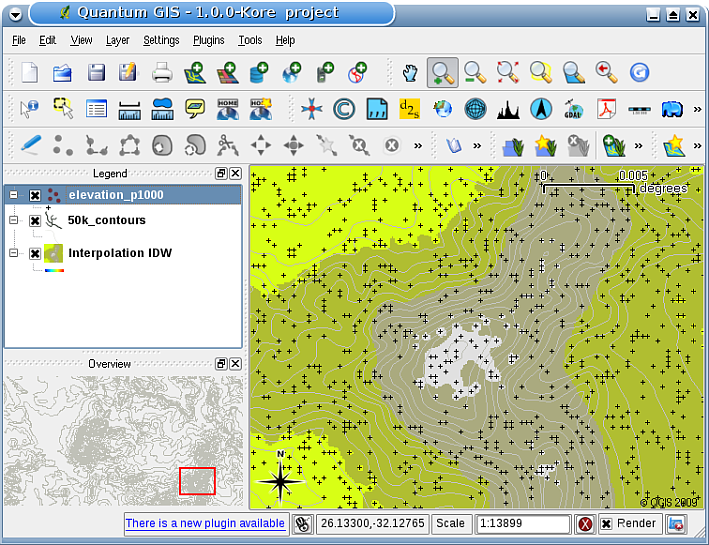
Fig. 11.39 မညီမညာ ကောက်ယူထားသော အမြင့် နမူနာ point များ (အနက်ရောင် ကြက်ခြေခတ်များဖြင့် ပြသထားသည့်) မှရရှိလာသော IDW interpolation ရလာဒ်

11.4. Triangulated Irregular Network (TIN)

TIM interpolation သည် GIS တွင် နာမည်ကြီးသော နောက်ထပ် tool တစ်ခုဖြစ်ပါသည်။ အသုံးများသော TIN algorithm ကို Delaunay triangulation ဟုခေါ်ပါသည်။ ၎င်းသည် အနီးအနားနီးစပ်ရာ point များကို တြိဂံဖွဲ့ပေးပြီး မျက်နှာပြင်တစ်ခုကို ဖန်တီးပေးနိုင်ရန် ကြိုးပမ်းပါသည်။ ထိုသို့လုပ်ဆောင်ရန် ရွေးချယ်ထားသောနမူနာ point များပတ်လည်တွင် circumcircle (စက်ဝိုင်း) များဖန်တီးပြီး စက်ဝိုင်းများ ထိဖြတ်သောနေရာများကို ချိတ်ဆက်ပေးကာ တြိဂံများရနိုင်သမျှရအောင် ဆောင်ရွက်ရပါသည် (Fig. 11.40 တွင်ကြည့်ပါ)။

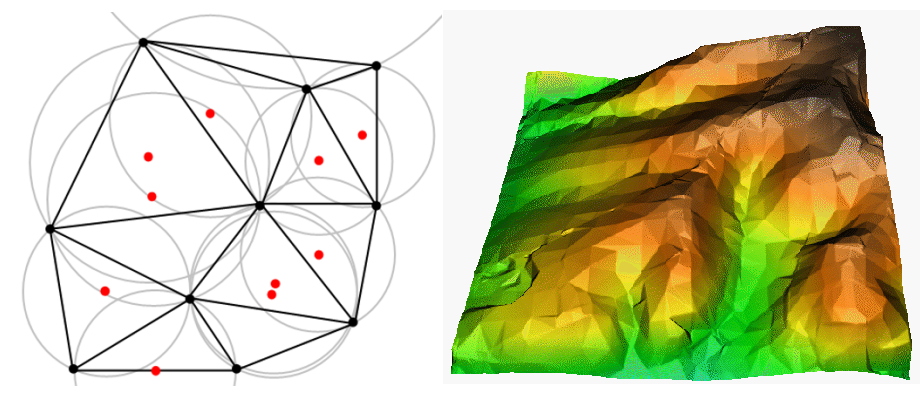
Fig. 11.40 အနီရောင်နမူနာ data များပတ်လည်ရှိ စက်ဝိုင်းများဖြင့် Delaunay triangulation။ ညာဘက်ပုံသည် အမြင့် vector point များမှ ဖန်တီးထားသော TIN surface ရလာဒ်ပုံဖြစ်သည်။ ဓာတ်ပုံရင်းမြစ်- Mitas, L., Mitasova, H. (1999)။

TIN interpolation ၏အဓိက အားနည်းချက်မှာ မျက်နှာပြင်သည် ချောမွေ့မနေပဲ လွှသွားပုံ အချွန်အတက်ပုံစံဖြစ်နေပါသည်။ ထိုသို့ဖြစ်ရခြင်းမှာ တြိဂံအစွန်းများရှိ တစ်ဆက်တစပ်တည်းမဟုတ်သော လျှောစောက်များနှင့် နမူနာ data point များကြောင့် ဖြစ်သည်။ ထို့အပြင် trigulation နည်းလမ်းသည် နမူနာ data point ကောက်ယူသည့်ဧရိယာကိုကျော်လွန်ပြီး ခန့်မှန်းတွက်ချက်ရန်အတွက် ယေဘုယျအားဖြင့် သင့်လျော်မှုမရှိပါ (Fig. 11.41 တွင်ကြည့်ပါ)။

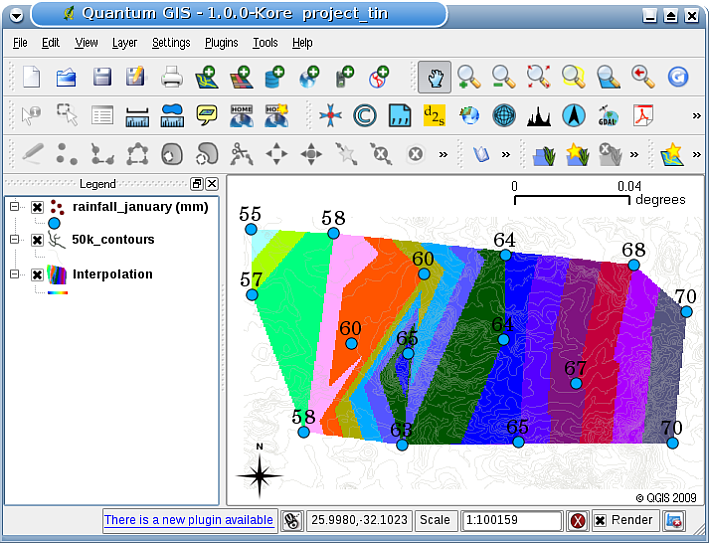
Fig. 11.41 မညီမညာကောက်ယူထားသော မိုးရေချိန်နမူနာ point (အပြာရောင်စက်ဝိုင်းများ) များမှဖန်တီးထားသော Delaunay TIN interpolation ရလာဒ်

11.5. အဖြစ်များသောပြဿနာများ/သတိထားရမည့်အရာများ (Common problems / things to be aware of)

အခြေအနေအားလုံးတွင် အသုံးပြုနိုင်သည့် တစ်ခုတည်းသော interpolation နည်းလမ်းမျိုး မရှိသည်ကို မှတ်သားထားပါ။ အချို့နည်းလမ်းများသည် ပိုမိုတိကျပြီးအသုံးဝင်သော်လည်း တွက်ချက်ချိန်ကြာမြင့်ပါသည်။ ၎င်းတို့အားလုံးတွင် အားနည်းချက်များနှင့် အားသာချက်များရှိကြပါသည်။ အသုံးပြုမည့် နမူနာ data ၊ ထုတ်ယူမည့် မျက်နှာပြင်အမျိုးအစား နှင့် ခန့်မှန်းအမှားများကို လက်ခံနိုင်မှု အပေါ်တွင်မူတည်၍ လက်တွေ့တွင် interpolation နည်းလမ်းတစ်ခုကို ရွေးချယ်သင့်ပါသည်။ ယေဘုအားဖြင့်ဆိုရလျှင် အောက်ပါအဆင့် ၃ ဆင့်ကို အကြံပြုပါသည်-

1. နမူနာ data များအား အကဲဖြတ်ပါ။ ထိုသို့လုပ်ဆောင်ခြင်းဖြင့် ဧရိယာထဲတွင် data များမည်ကဲ့သို့ ပြန့်နှံ့နေသည်ကို သိရှိနိုင်မည်ဖြစ်ပြီး မည်သည့် interpolation နည်းလမ်းကို အသုံးပြုရမည်ကို သိစေနိုင်မည်ဖြစ်သည်။

2. နမူနာ data နှင့် လေ့လာမှုရည်ရွယ်ချက် နှစ်မျိုးစလုံးနှင့် အသင့်တော်ဆုံးဖြစ်သော interpolation နည်းလမ်းတစ်ခုကို အသုံးချပါ။ မသေချာပါက နည်းလမ်းများစွာကို ကြိုးစားစမ်းကြည့်ပါ။

3. ရလာဒ်များကို နှိုင်းယှဉ်ကြည့်ပြီး အကောင်းရလာဒ်နှင့် အသင့်တော်ဆုံးနည်းလမ်းကို ရှာဖွေပါ။ အစပိုင်းတွင်တော့ အချိန်ပေးရမည့် လုပ်ငန်းစဉ်ဟု ထင်ရပါလိမ့်မည်။ သို့သော် အမျိုးမျိုးသော interpolation နည်းလမ်းများအကြောင်း အတွေ့အကြုံနှင့်ဗဟုသုတ ရရှိလာသည်နှင့်အမျှ အသင့်တော်ဆုံး surface ကိုထုတ်ယူရန် ကြာချိန်သည် များစွာလျော့နည်းသွားပါလိမ့်မည်။

11.6. အခြားသော interpolation နည်းလမ်းများ (Other interpolation methods)

ဤအခန်းတွင် IDW နှင့် TIN interpolation နည်းလမ်းများကိုသာ အဓိကထားပြသခဲ့သော်လည်း GIS ထဲတွင်အသုံးပြုနိုင်သော အခြား interpolation နည်းလမ်းများစွာရှိပါသည်၊ ဥပမာ- Regularized Splines with Tension (RST) ၊ Kriging သို့မဟုတ် Trend Surface interpolation တို့ဖြစ်သည်။ အောက်တွင်ရှိသော နောက်ထပ်ဖတ်ရမည်များ ကဏ္ဍတွင် ဝက်ဘ်ဆိုဒ်လင့်ခ် တစ်ခုရှိပါသည်၊ ထို လင့်ခ်တွင် ကြည့်ပါ။

11.7. လေ့လာခဲ့ပြီးသည့်အရာများ (What have we learned?)

ဤစာမျက်နှာတွင် ဖော်ပြခဲ့သည်တို့ကို အကျဉ်းချုပ်ဆိုရသော်-

• Interpolation သည် တန်ဖိုးသိပြီးသား vector point များကိုအသုံးပြု၍ မသိသေးသည့်တည်နေရာများရှိ တန်ဖိုးများကို ခန့်မှန်းတွက်ချက်ပြီး ဧရိယာတစ်ခုလုံးကိုလွှမ်းခြုံသော raster surface ကို ဖန်တီးပေးပါသည်။

• Interpolation ရလာဒ်သည် raster layer တစ်ခုဖြစ်သည်။

• မသိရသေးသည့်တည်နေရာများအတွက် တန်ဖိုးများကို အကောင်းဆုံးခန့်မှန်းရန် သင့်တော်သော interpolation နည်းလမ်းကိုရှာဖွေရန် အရေးကြီးပါသည်။

• IDW interpolation သည် နမူနာ point များတွင် weight ပြုလုပ်ပေးပါသည်၊ သို့မှသာ ခန့်မှန်းမည့် point နှင့်အကွာအဝေး ဝေးကွာလေလေ နမူနာ point ၏လွှမ်းမိုးမှုလျော့နည်းလေလေ ဖြစ်ပါမည်။

• TIN interpolation သည် နမူနာ point များကိုအသုံးပြုပြီး အနီးဆုံးအနီးအနားရှိ point အချက်အလက်ပေါ်အခြေခံထားသော တြိဂံများဖြင့် ဖွဲ့စည်းထားသည့် surface တစ်ခုကို ဖန်တီးပေးပါသည်။

11.8. ယခု သင်တို့ ကြိုးစားကြည့်ပါ! (Now you try!)

အောက်ပါတို့မှာ သင်တန်းသားများအား ကြိုးစားကြည့်စေရန် အချက်တစ်ချို့ဖြစ်ပါသည်-

• စိုက်ပျိုးရေးဦးစီးဌာနသည် သင့်ဧရိယာထဲရှိ မြေအသစ်တွင် စိုက်ပျိုးမှုလုပ်ဆောင်ရန် စီစဉ်နေပါသည်၊ မြေဆီလွှာ၏ ဝိသေသလက္ခဏာများကို မကြည့်ပဲ ထွက်နှုန်းကောင်းမွန်စေမည့် လုံလောက်သည့် မိုးရေချိန် ရမရကို သိလိုပါသည်။ သူတို့တွင်ရှိသော အချက်အလက်များအားလုံးသည် ထိုဧရိယာပတ်လည်ရှိ မိုးလေဝသစခန်းအနည်းငယ်မှ ရယူထားပါသည်။ အမြင့်ဆုံးမိုးရေချိန်ရရှိနိုင်မည့် ဧရိယာများကိုပြသပေးသော interpolate ပြုလုပ်ထားသည့် surface တစ်ခုကို သင်တန်းသားများနှင့်အတူ ဖန်တီးကြည့်ပါ။

• ခရီးသွားလုပ်ငန်းရုံးသည် ဇန်နဝါရီ နှင့် ဖေဖော်ဝါရီလရှိ ရာသီဥတုအခြေအနေများအကြောင်း အချက်အလက်များထုတ်ပြန်လိုပါသည်။ ရုံးတွင် အပူချိန်၊ မိုးရေချိန်နှင့် လေတိုက်နှုန်း data များရှိပြီး ထို data များကို interpolate လုပ်ဆောင်ကာ ခရီးသွားများအတွက် မပူမအေးလွန်းသည့်အပူချိန်ရှိသော၊ မိုးမရွာပဲ လေတိုက်နှုန်းအနည်းသာရှိသော အကောင်းဆုံးရာသီဥတုအခြေအနေရှိနိုင်မည့် နေရာများကို ခန့်မှန်းတွက်ထုတ်စေလိုပါသည်။ သင့်ဒေသအတွင်း ထိုသတ်မှတ်ချက်များနှင့်ကိုက်ညီသော ဧရိယာများကို ဖော်ထုတ်နိုင်ပါသလား။

11.9. စဉ်းစားရမည့်အချက် (Something to think about)

သင့်တွင် ကွန်ပျူတာမရှိပါက topo မြေပုံတစ်ခုနှင့် ပေတံတစ်ချောင်းကို အသုံးပြုပြီး ကွန်တိုမျဉ်းများအကြား အမြင့်တန်ဖိုးများကို ခန့်မှန်းပါ သို့မဟုတ် စိတ်ကူးထဲရှိသော မိုးလေဝသစခန်းများအကြား မိုးရေချိန်တန်ဖိုးများကို ခန့်မှန်းပါ။ ဥပမာ- မိုးလေဝသခစန်း A ရှိ မိုးရေချိန်သည် ၅၀ မီလီမီတာရှိပြီး မိုးလေဝသစခန်း B ရှိမိုးရေချိန်သည် ၉၀ မီလီမီတာရှိပါက စခန်း A နှင့် စခန်း B ကြားရှိ အကွာအဝေးတစ်ဝက်တွင်ရှိသော မိုးရေချိန်သည် ၇၀ မီလီမီတာ ဖြစ်ကြောင်း သင်ခန့်မှန်းနိုင်ပါသည်။

11.10. နောက်ထပ်ဖတ်ရှုရမည်များ (Further reading)

စာအုပ်များ:

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986

• DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195

• Mitas, L., Mitasova, H. (1999). Spatial Interpolation. In: P.Longley, M.F. Goodchild, D.J. Maguire, D.W.Rhind (Eds.), Geographical Information Systems: Principles, Techniques, Management and Applications, Wiley.

Websites:

• https://en.wikipedia.org/wiki/Interpolation

• https://en.wikipedia.org/wiki/Delaunay_triangulation

QGIS ထဲတွင်အသုံးပြုနိုင်သော interpolation tool များနှင့်ပတ်သက်၍ QGIS အသုံးပြုသူလမ်းညွှန်ထဲတွင် ပိုမိုအသေးစိတ်ဖော်ပြထားပါသည်။

11.11. နောက်ထပ်ဘာအကြောင်းအရာလဲ (What’s next?)

ဤခေါင်းစဉ်သည် နောက်ဆုံးစာမျက်နှာဖြစ်ပါသည်။ QGIS ကိုသုံးစွဲကြည့်ရန်နှင့် GIS software ဖြင့်လုပ်ဆောင်နိုင်သော အခြားသောအရာများအားလုံးကိုရှာဖွေနိုင်ရန် QGIS အသုံးပြုသူလမ်းညွှန်ကိုအသုံးပြုကြရန် တိုက်တွန်းလိုပါသည်။